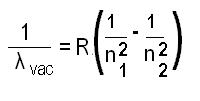What is the Rydberg formula for any hydrogen-like chemical elements?
In atomic physics, The Rydberg formula is used to describe the wavelengths of spectral lines of many chemical elements.
The modified Rydberg formula given below is used for any hydrogen-like chemical elements.
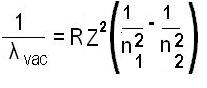
λvac= the wavelength of the light emitted in vacuum;
R = the Rydberg constant for this element;
Z = the atomic number, i.e. the number of protons in the atomic nucleus of this element;
n1and n2= integers such that n1< n2, corresponding to the principal quantum numbers of the orbitals occupied before and after.
posted in Atoms, Molecules and Nuclei | Comments Off on What is the Rydberg formula for any hydrogen-like chemical elements?