What is the formula for acceleration of a body rolling down a smooth inclined plane?
Posted in Rotational Motion | Email This Post
|
Email This Post
|
Consider a body of mass (M) and radius (R) rolling down (without slipping) a smooth inclined plane making an angle of inclination (Θ). When a body rolls down its Potential Energy ( resting at the top of inclined plane) is converted into the Kinetic energy of translation as well as rotation. As we know that body is rolling down a smooth inclined plane this means there will be no loss of energy due to friction. So the loss in Potential Energy is same as gain in kinetic energy.
Loss in potential Energy = Gain in kinetic energy
Mgh = ½ (M v2) + ½ (I ω 2)
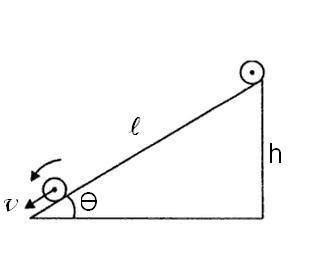
From the above fig we know that h = ℓ sin Θ, substituting this in the above equation we get,
Mg ℓ sin Θ = ½ (M v2) + ½ (I ω 2)
Mg ℓ sin Θ = ½ (M v2) + ½ (M K2 .(v2 / R 2) )
Where K = radius of gyration, ω = v/R and I = M K2
Mv2 / 2 (1 + (K2 / R2)) = Mg ℓ sin Θ
v2 = 2 g ℓ sin Θ / (1 + (K2 / R2)) but v2 = 2aℓ
So Formula for acceleration of a body rolling down a smooth inclined plane,
a = g sin Θ / (1 + (K2 / R2))

your website is very useful to every student thanks for making this website ok dear