Consider a body of mass (M) and radius (R) rolling down (without slipping) a smooth inclined plane making an angle of inclination (Θ). When a body rolls down its Potential Energy ( resting at the top of inclined plane) is converted into the Kinetic energy of translation as well as rotation. As we know that body is rolling down a smooth inclined plane this means there will be no loss of energy due to friction. So the loss in Potential Energy is same as gain in kinetic energy.

Loss in potential Energy = Gain in kinetic energy

Mgh = ½ (M v²) + ½ (I ω ²)

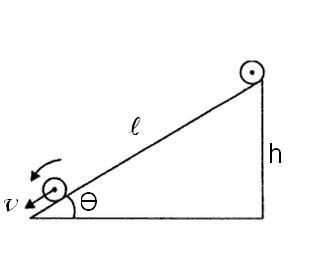
From the above fig we know that h = ℓ sin Θ, substituting this in the above equation we get,
Mg ℓ sin Θ = ½ (M v²) + ½ (I ω ²)
Mg ℓ sin Θ = ½ (M v²) + ½ (M K² .(v² / R ²) )
Where K = radius of gyration, ω = v/R and I = M K²

Mv² / 2 (1 + (K² / R²)) = Mg ℓ sin Θ

v² = 2 g ℓ sin Θ / (1 + (K² / R²)) but v² = 2aℓ

So Formula for acceleration of a body rolling down a smooth inclined plane,

a = g sin Θ / (1 + (K² / R²))

Law of conservation of angular momentum is stated as “If the total external torque acting on a body is zero, the total angular momentum of that body remains constant or conserved”. This means that the angular momentum of that body remains same in absence of external torque.

According to the Law of conservation of angular momentum

         Angular momentum = I₁ω_{1 =} l₂ω₂= constant

I₁ and ω₁ are the initial moment of inertia and angular velocity of a rotating body

I₂ and ω₂ are new moment of inertia and angular velocity of the body

A rigid body rotates about a fixed axis. The rigid body consists of a large number of particles.
Let m1, m2, m3 etc., be the masses of the particles situated at distances r1, r2, r3 , … etc., from the fixed axis. All the particles rotate with the same angular velocity, but with different linear velocities depending on the values of ‘r’.
The angular momentum of a rigid body (L) = m₁ r₁²ω ₊  m₂ r₂²ω…
The angular momentum of a rigid body (L) = (m₁ r₁² + m₂ r₂²….) ω

The angular momentum of a rigid body (L) = Σ mr²ω …………………(1)

But, Σmr² = moment of inertia of the rigid body = I

Therefore,

Angular momentum of a Rigid body = I × ω……putting value of I in (1)

Angular momentum of a Rigid body = moment of inertia of the rigid body ( I) x × angular velocity (ω)

The S.I. unit for angular momentum is kgm²rad/s or kgm³/s

The moment of linear momentum is known as angular momentum. In other words the rotational analog of linear momentum is known as angular momentum
Consider a particle of mass m at a distance r from the axis of rotation. When a particle is in rotational motion about an axis, it has both linear velocity ‘v’ and angular velocity ‘ω’.

Angular momentum of the particle = linear momentum x perpendicular distance between
the particle and the axis of rotation or radius (r)

We know that momentum = mass × velocity
Substituting the value of momentum in the above equation we get,
Angular momentum = m v × r
we know that relation between Linear velocity and Angular velocity is defined as
Linear velocity (v) = Radius (r) x Angular velocity (ω)

Substituting the values we get
Angular momentum = m × (r. ω) × r
Therefore, the formula for Angular momentum is given as,
Angular momentum = mr²ω
The S.I. unit for angular momentum is kgm²s^-1

Torque is defined as the rate of change of angular momentum of an object. The definition of torque states that one or both of the angular velocity or the moment of inertia of an object are changing.
The formula for Torque acting on a body is given as,

Torque (τ) = moment of inertia (I) × angular acceleration (α)
→             →
τ     = I x α  

where τ = Torque
α = angular acceleration
I = moment of inertia
S.I. unit of torque is Newton metre (Nm)